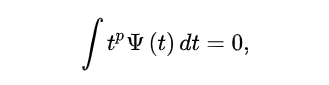小波分析具体理解

简介

小波分析继承和发展了短时傅立叶变换局部化的思想，同时又克服了窗口大小不随频率变化等缺点，能够提供一个随 频率 改变的“时间-频率”窗口，是进行信号时频分析和处理的理想工具。

小波函数不同于傅里叶变换的正弦波函数，它是个快速衰减并且有限长的波函数，同时满足 积分为 0 的条件。

能对时间（空间）频率的 局部化分析，通过 伸缩平移 运算对信号（函数）逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能 自动适应 时频信号分析的要求，从而可聚焦到信号的任意细节，解决了Fourier变换的困难问题，成为继Fourier变换以来在科学方法上的重大突破。

小波变换的作用

通过变换能够充分 突出 问题某些方面（信号）的 特征 。

小波变换

小波变换的定义如下：

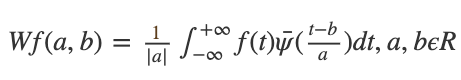
f(t)为被分析的信号，phi(t-b/a)为小波函数，phi(t-b/a)通过 平移 在每一个点上求它们的乘积，并且求积分。这就是小波变换的整个过程。

CWT 连续小波变换

小波函数与原信号对应点相乘，再相加，得到对应点的小波变换系数，平移小波基函数，再计算小波函数与原信号对应点相乘，再相加，这样就得到一系列的小波系数。

DWT 离散小波变换

实际上，离散小波变换是对连续小波变换的 尺度、位移 按照 2 的幂次进行离散化得到的。

重要概念

小波系数： 小波基函数 与 原信号 相似的系数，是小波分解中的一些参数，通过这些参数可以重构得到原始信号。

基本小波（母小波函数）：是一具有特殊性质的实值函数，是具有快速衰减的波函数(有限长)，在数学上满足 积分为 0 的条件。

小波函数（小波基函数）：通过将母小波函数 伸缩、平移 得到的。

尺度函数：通过一个母小波函数改变 伸缩 、平移 两个参数得到的 所有 小波函数的函数，可以以这 一组尺度函数 来代表原来的信息。

支撑长度：表示 滤波器 的长度（滤波的频率范围），滤波器的长度越短，小波变换的计算量就越低。

消失矩：对 基本小波 施加所谓的 消失矩 条件，使尽量多的 小波系数 为 0 或者产生尽量 少 的非零小波系数，这样有利于数据压缩和消除噪声。消失矩 越高，高频子带的小波系数越小，并且接近 0 的 小波系数 越多。

紧支撑小波：若函数在 [a,b] 外恒为 0，则称该函数 紧支撑 在这个区间上，具有该性质的小波称为 紧支撑小波。

其中，phi(t) 为基本小波，0 <= p < N*。则称小波函数具有 *N 阶消失矩。从上式还可以得出，同任意 n-1 阶多项式正交。

小波的消失矩特性使函数在 小波展开 时消去了其 高阶平滑部分，因此 小波系数 将仅仅反映函数的 高阶变化部分，使我们能研究函数的高阶变化和某些高阶导数中可能的奇异性信息。

一般来说，这个消失矩的数字越大，这个小波越 光滑（长的小波滤波器）

小波分解与重构

小波分解的意义就在于能够在 不同尺度 上对信号进行分解，而且对不同尺度的选择可以根据不同的目标来确定。

对于许多信号，低频 成分相当重要，它常常蕴含着信号的特征，而 高频 成分则给出信号的细节或差别。人的话音如果去掉 高频 成分，听起来与以前可能不同，但仍能知道所说的内容；如果去掉足够的 低频 成分，则听到的是一些没有意义的声音。

小波重构是用处理后的系数重构信号。

Daubechies(dbN) 小波

dbn 中 n 表示 消失矩

支撑长度为 2n-1

小波滤波器 的长度 = 2n
s
其理论意义在于，如果你感兴趣的信号在一个区间上是一个 N 阶多项式的形式，并且使用消失矩为 N 的小波，这个小波系数在这个区间内将会是 0

消失矩为 N 的小波正交于最多 N 阶多项式。

因此，如果一个多项式信号的阶数最高是 1 的话，在一个区间上一个 ‘db1’ 小波的小波系数是 0。

持续更新。