Fourier分析：Fourier级数 + Fourier变换

傅里叶分析

傅立叶分析的作用是把 一个函数 分解为 许多三角函数的和 的形式。

这些三角函数的频率都是某个基频的整数倍。如果这个基频无限趋近于0，那么在极限的情况下这函数的频率就连续了，将连续 时域 函数映射到连续的 频域 函数的变换就是标准的傅立叶变换。

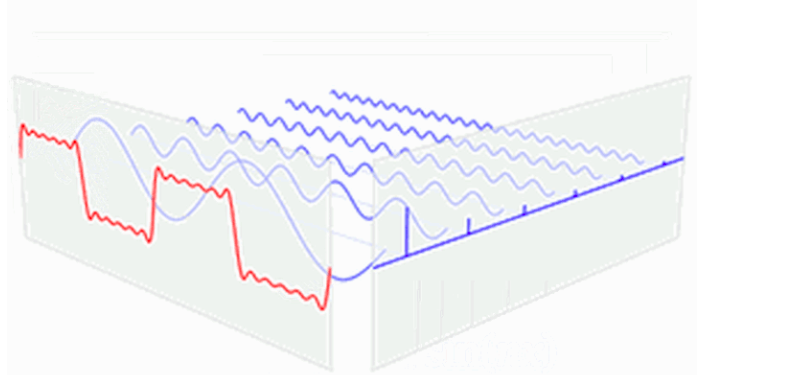
由于工程采集的信号大多都是离散的，把时域离散化以后不可能在得到连续的频域函数，所以在频域上也不连续了，这种离散时域序列到离散频域序列的变换称之为离散傅立叶变换(DFT)。

Fourier分析的主要内容：Fourier级数 + Fourier变换 两个方面。

傅里叶级数

下面是傅里叶级数最基本的形式👇

L²(0, 2π)表示在实数集 R 上以 2π 为周期且在 (0, 2π) 上 平方可积函数 的全体。

L¹(0, 2π)表示在实数集 R 上以 2π 为周期且在 (0, 2π) 上 绝对可积函数 的全体。

在L²(0, 2π)中定义内积为

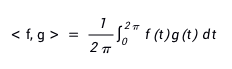
如果 <f, g> = 0, 则 f, g 是正交的。(可过滤)

令 g => e^ikt, 函数集{e^ikt}(k∈Z)是L²(0, 2π)的标准正交基，使L²(0, 2π)中的任意 函数 都能展成Fourier级数。

通过泰勒展开公式可得，sin(wt) + cos(wt) = e^iwt）

傅里叶变换

设 f(t) 是定义在 R 上的函数，f(t) 的 Fourier 变换定义为👇

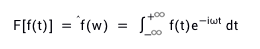
Fourier变换能够较好地刻画信号的 频率(ω) 特性，但不能提供信号在时频(t)上的任何 局部信息。以上面定义可见，Fourier变换使用信号在时域中的全部信息。但许多情况下，我们感兴趣的信号往往是局部的，然后使用Fourier变换，信号的 时域信息 相当于丢失了，很难知道时间发生的确切时间。

而小波变换解决了Fourier变换的这些不足。